Causality

What is Causality? (Work in Progress)

Causality indeed has many meanings, but all of them are connected in some sense. The concept of causation exists in ancient Greece philosophy. The metaphysical notion of causality is before the notions of space and time. It was the great philosopher Plato(423 BC) who put forward the idea of causation, he viewed causes as things (not like states or events), but the things with information. He argues about the presupposition of what can or cannot be considered as a cause, which all humans perceive. Later the idea was causation was philosophically and mathematically expanded by Aristotle, Hobbes, Spinoza, and many more. Many researchers tried to associate causation to the question like ‘What is this?’, ‘What is this made of?’, ‘Who is this made by?’, ‘What is this made for?’, and ‘What is it that makes this what it is and not something else?’. It’s fascinating to notices the existence of these questions from around 400 BC.

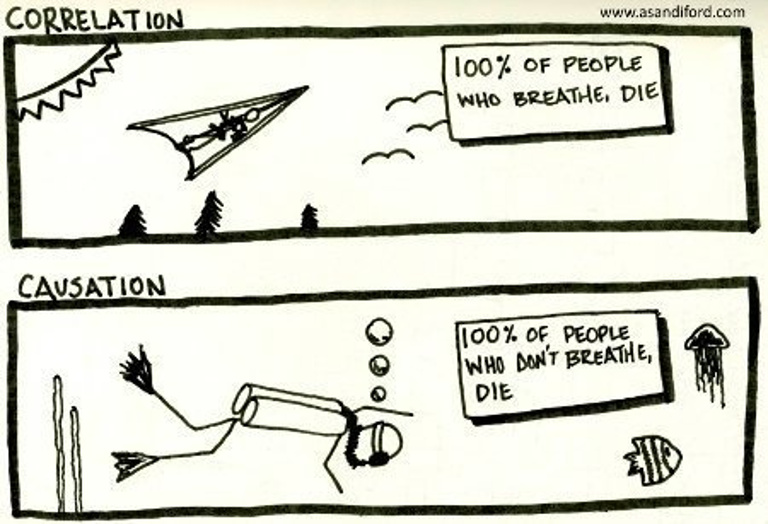
The above figure elegantly captures the idea of causality and how it’s different from correlation. It’s quite common that human decisions are biased by correlation rather than causality. To elaborate, correlation is a kind of spurious associations. From the above image, it’s wrong to conclude that breathing is the reason for death, though 100% of cases exhibit that behavior. Causality is often misleading or misunderstood; causality can be considered as correlation only in a very controlled setting, i.e., when determining causal relation between two variables A and B, it can be considered as the correlation between two variables when conditioned on all other variables (direct or confounding). Quantification of these methods is again a tricky and challenging task.

Causality: Statistical viewpoint

Many scientists divided the causality into many levels; each level encodes some aspect of causation. The study of causality and causation from a statistical viewpoint was started in 1950s. Good in initial years of his research established the definition of level-0 causality, which is the statistical association between cause and effect between two variables without marginalizing or conditioning on other variables. In level-1, causality is based on the interventional study, where an alternative hypothesis is imposed and evaluated for the outcome. Lastly, we have level-2 causality, which deals with carefully designed experiments using generative distributions.

In the past couple of decades, the causality has taken its lead in the analysis of machine learning models. It was by Judea Pearl, causal inference took a very new form. Based on his formulation again, causality has 3 different levels (i) Associations, (ii) Interventions, and (iii) Counterfactuals, where each of them captures different types of information.

(i) Level-0 Association: Association can directly be linked to conditional expectations, and they are at the bottom line of the causal hierarchy. The association address the question of ‘What is _?’. From the above example, consider the statement “100% of people who breathe, die”, here, the event of breathing is associated with the event of a death in a random sense. This still an association but doesn’t provide us any information about the system in general, So they are sporous associations. Now consider the statement “100% of people who don’t breathe, die”, here, the events are death and not-breathing. But here they are causally linked, here the event of not breathing is directly associated to death.

Mathematically above statements can be expressed as: (a) “100% of people who breathe, die”: \(\mathbb{P}(death~/~(they~breath)) = anything\) because they are correlated, but they don’t possess any causal link. (b) “100% of people who don’t breathe, die”: \(\mathbb{P}(death~/~ (they~don't~breath)) = 1.0\) as they are directly associated.

(ii) Level-1 Intervention: Intervention can be considered as outcomes of made up experiment. When the conditioning variable changes, the evidence or support of the statement may increase or decrease. Interventions address the questions of ‘What if _?’. As proposed by Pearl Interventions deals with do-calculus, mathematically \(\mathbb{P}(death~/~ do(accidents)) = .6\). Here, the conditional variable is intervened with an event of accidents; the probability of death reduces from the previous case (\(\mathbb{P}(death~/~ (they~don't~breath)) = 1.0\)).

(iii) Level-2 Counterfactuals: Counterfactuals are considered at the top level of hierarchy in causal analysis. Counterfactuals deal with retrospective reasoning, i.e., to ask negative questions. Often counterfactual reasoning involves working with joint distribution, where you ask a question of \(\mathbb{P}(eventC ~/~ eventA and eventB)\), in both association and intervention work with conditionals but this requires joint distribution. Due to this reason, this supersedes both levels.

Measure Causality

Causality is an objective quantity, but measuring causality is puzzling and often misleading. The above methods help in analyzing causal relations between multiple events, but to measure causality, we need to follow different procedures. It was during 1969; Economist Clive Granger proposed one such method called G-Causality to quantify causation. According to G-causality eventA can be considered as cause for eventB if the future realizations of eventB can be explained by the past realizations of the joint (eventA and eventB), rather than using any one alone. A similar idea was expressed in information theory in terms of transfer entropy concept, which models the flow of information as a flow of entropy from one form to another. It has been proven that both G-causality and transfer entropy results in the same objective definition of causation.

Deep Learning

Deep learning inherently learns correlation rather than any sort of causation. The above image depicts the risk of just learning correlation. Current deep learning models are build by correlative building blocks, i.e., the basic building blocks of CNN is convolution (spatial cross-correlation), which encodes information from the input data based on correlations; this continues till the extraction of higher-order features. Whatever the state-of-the-art, may the current deep learning models be at the end of the day they are just correlation-based engines. Someday, everyone jumps off the bridge…

We can find lots of research in finding adversarial examples, i.e., just by manipulating the image with unnoticeable noise can scrap the entire deep learning system. The above figure illustrates the same effect. The noise pattern doesn’t bring any drastic change in an image (it’s not even noticeable to human eyes). Again, these noise patterns are carefully designed, but it’s not hard to design hardware which captures images with these noise patterns. The possible way is to encourage causal learning, which is to change the building blocks of deep learning, to use something which is driven by causation rather than cross-correlation.

In the end, to push deep learning models towards causality, the way would be to encode causal information in the building blocks rather than post-training analysis.

References

• https://ftp.cs.ucla.edu/pub/stat_ser/r350.pdf
• https://bayes.cs.ucla.edu/home.htm
• https://ftp.cs.ucla.edu/pub/stat_ser/r481.pdf
• https://arxiv.org/pdf/1912.03277.pdf
• https://proceedings.mlr.press/v97/chattopadhyay19a/chattopadhyay19a-supp.pdf
• https://www.math.chalmers.se/~wermuth/pdfs/papcaus.pdf
• https://arxiv.org/pdf/1401.1457.pdf