Conditional Probability theorems
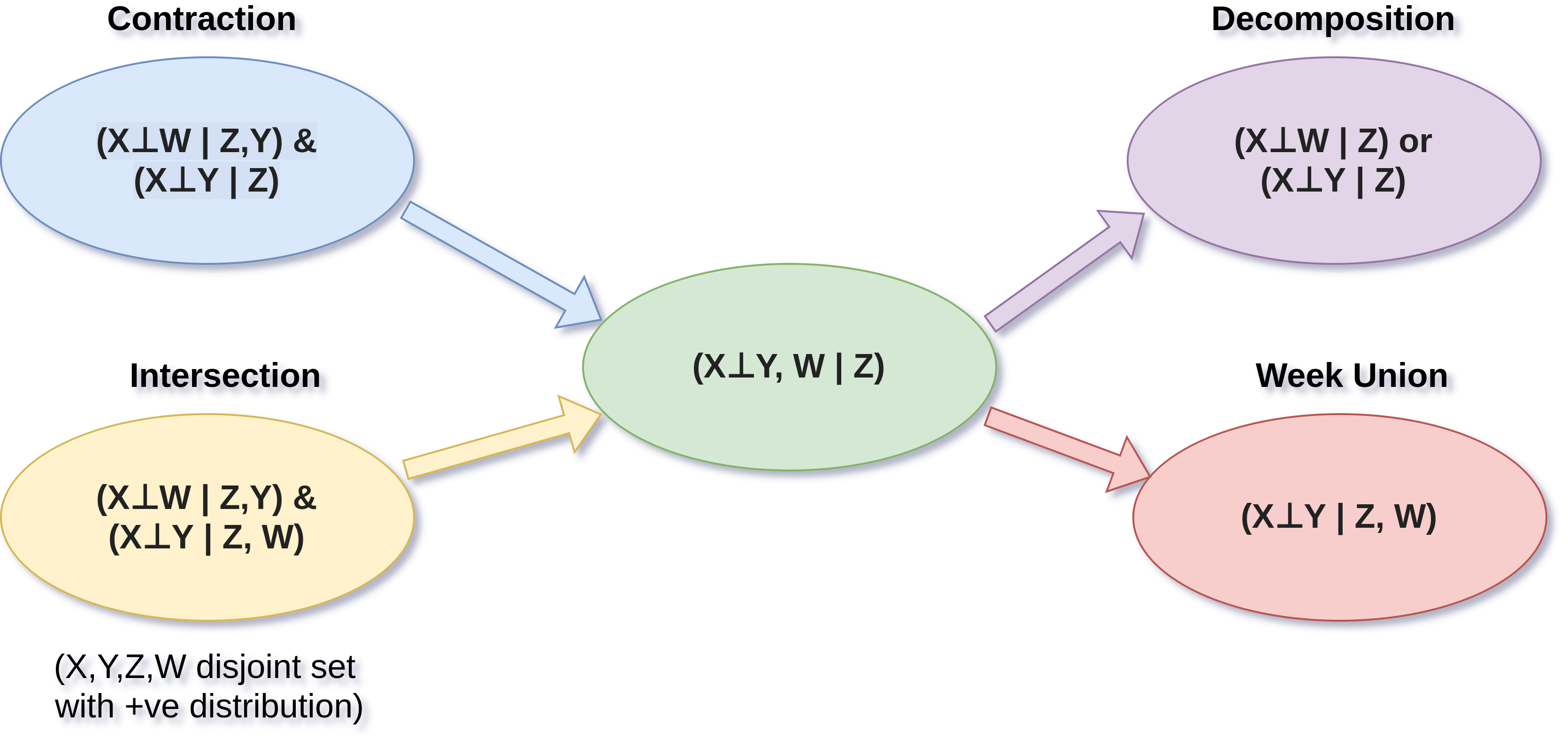
Contraction
Given: \((X\perp W~|~Z,Y) ~\&~ (X \perp Y~|~Z)\)
To show: \((X \perp Y, W ~|~Z)\)
Proof:
\[\sum_W \mathbb{P}(X, W, Y~|~Z) = \mathbb{P}(X ~|~ Z)\mathbb{P}(Y~|~Z)\] \[\Rightarrow \mathbb{P}(X, Y~|~Z) = \mathbb{P}(X ~|~ Z)\mathbb{P}(Y~|~Z)\]By Bayes Theorem:
\[\mathbb{P}(X,Y~|~Z) = \frac{\mathbb{P}(X~|~Z,Y)\mathbb{P}(Z,Y)}{\mathbb{P}(Z)}\]Based on given conditions:
\[\mathbb{P}(X, W~|~Z,Y) = \mathbb{P}(X ~|~ Z,Y)\mathbb{P}(W~|~Z,Y)\] \[\mathbb{P}(X~|~Z)\mathbb{P}(Y~|~Z)\mathbb{P}(Z)\mathbb{P}(W~|~Z,Y) = \mathbb{P}(X, W ~|~Z,Y)\mathbb{P}(Z,Y)\] \[\Rightarrow \mathbb{P}(X~|~Z)\mathbb{P}(Y~|~Z)\mathbb{P}(Z)\mathbb{P}(W~|~Z,Y) = \mathbb{P}(X, Y, W ~|~Z)\mathbb{P}(Z)\] \[\Rightarrow \mathbb{P}(X~|~Z)\mathbb{P}(W, Y~|~Z) = \mathbb{P}(X, Y, W ~|~Z)\] \[\Rightarrow (X \perp W,Y ~|~Z)\]Discussion:
Graph theory point of view:
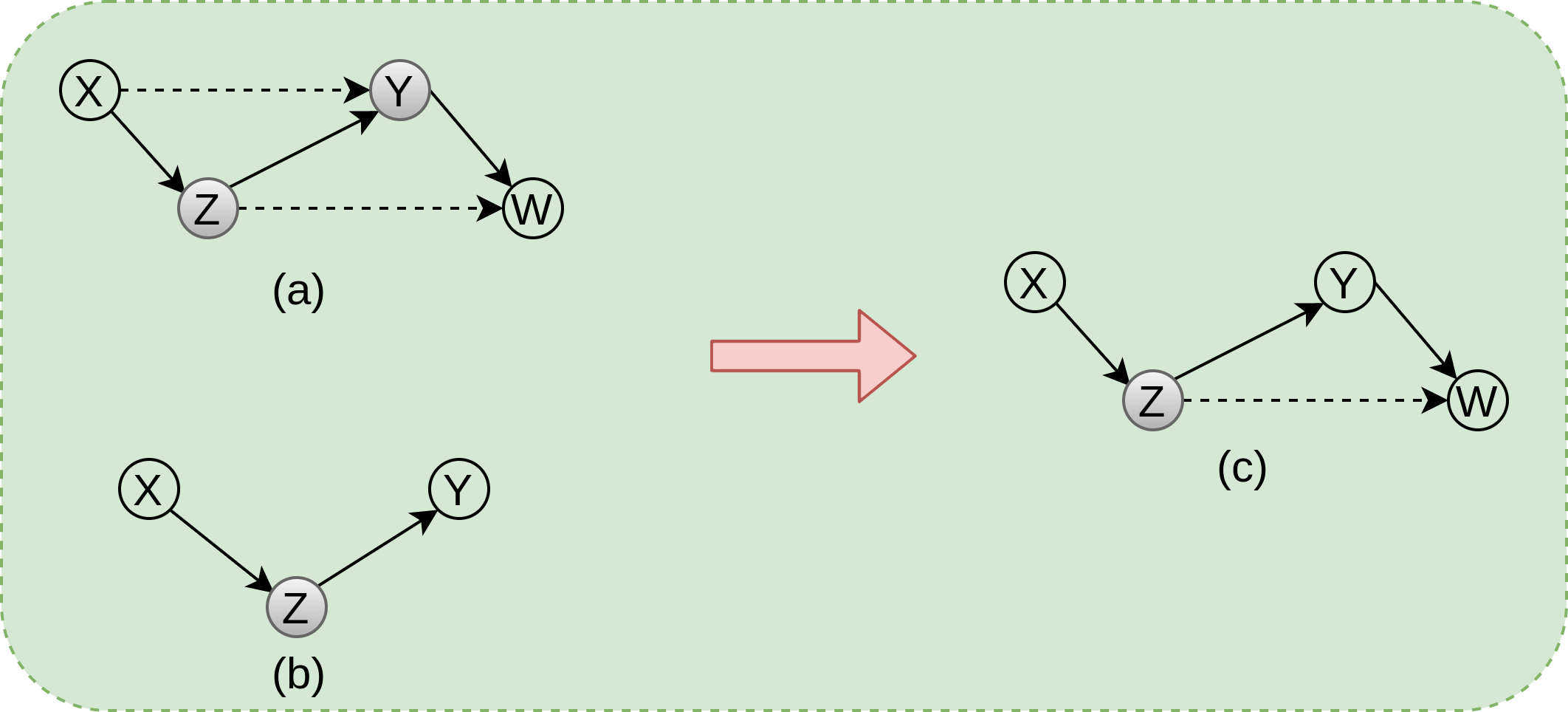
-
condition 1: \((X\perp W~/~Y,Z)\) implies there doesn’t exist any active trail running from X to W in the universe where Z and Y are known (or given)
-
In the below figure, (a) shows the graph incorporating above conditional independency
-
condition 2: \((X\perp Y~/~Z)\) implies there doesn’t exist any active trail running from X to Z in the universe where Z is known (or given). Subfigure (b) shows the graph incorporating this conditional independence
-
Combining above two conditions in the universe where Z is known, will result in subfigure (c) removing edge (X-Y)
-
In the subfigure (c), there doesn’t exist any active trail from X to Y, W, once Z is known. Which results in CI \((X\perp Y,W~/~Z)\)
Decomposition
Given: \((X\perp Y, W~|~Z)\)
To show: \((X \perp Y~|~Z)\) or \((X \perp W~|~Z)\)
Proof:
\[\mathbb{P}(X, Y, W~|~Z) = \mathbb{P}(X~|~Z) \mathbb{P}(Y,W~|~Z)\] \[\sum_W \mathbb{P}(X, Y, W~|~Z) = \sum_W \mathbb{P}(X~|~Z) \mathbb{P}(Y,W~|~Z)\] \[\Rightarrow \mathbb{P}(X, Y~|~Z) = \mathbb{P}(X~|~Z) \mathbb{P}(Y~|~Z)\] \[\Rightarrow (X\perp Y~|~Z)\]Similarly:
\[\sum_Y \mathbb{P}(X, Y, W~|~Z) = \sum_Y \mathbb{P}(X~|~Z) \mathbb{P}(Y,W~|~Z)\] \[\Rightarrow \mathbb{P}(X, W~|~Z) = \mathbb{P}(X~|~Z) \mathbb{P}(W~|~Z)\] \[\Rightarrow (X\perp W~|~Z)\]Discussion:
Graph theory point of view:
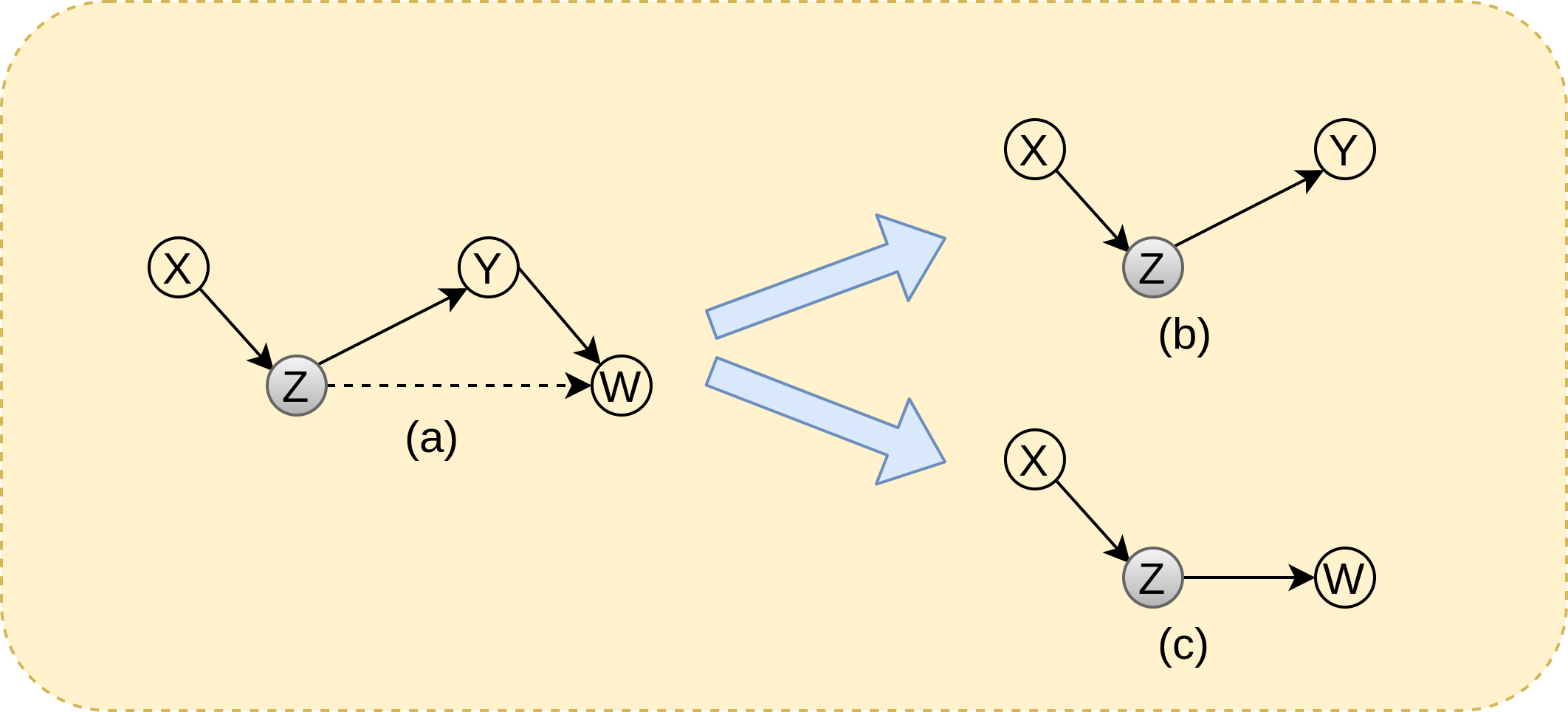
-
condition 1: \((X\perp W, Y~/,Z)\) implies there doesn’t exist any active trail running from X to W and Y in the universe where Z is known (or given)
-
In the below figure, (a) shows the graph incorporating above conditional independency
-
Once if the graph is marginalized over node Y or W, node X is independent of W or Y (unmarginalized variable)
-
In the subfigure (b, c), shows the conditional independencies obtained as a result of marginalization
Week Union
Given: \((X\perp Y, W~|~Z)\)
To show: \((X \perp Y~|~Z,W)\)
Proof:
\[\mathbb{P}(X, Y, W~|~Z) = \mathbb{P}(X~|~Z) \mathbb{P}(Y,W~|~Z)\]By Bayes Thm:
\[\mathbb{P}(X, Y~|~Z,W) = \frac{\mathbb{P}(X, Y, W, Z)}{\mathbb{P}(W, Z)}\] \[\Rightarrow \mathbb{P}(X, Y~|~Z,W) = \frac{\mathbb{P}(X, Y, W~|~ Z)\mathbb{P}(Z)}{\mathbb{P}(W, Z)}\]By Given condition:
\[\mathbb{P}(X, Y~|~Z,W) = \frac{\mathbb{P}(X~|~ Z)\mathbb{P}(Y,W~|~Z)\mathbb{P}(Z)}{\mathbb{P}(W, Z)}\]Again by Bayes Thm:
\[\mathbb{P}(X, Y~|~Z,W) = \frac{\mathbb{P}(X~|~ Z)\mathbb{P}(Y~|~W, Z)\mathbb{P}(W, Z)\mathbb{P}(Z)}{\mathbb{P}(Z)\mathbb{P}(W, Z)}\] \[\Rightarrow \mathbb{P}(X, Y~|~Z,W) = \mathbb{P}(X~|~ Z)\mathbb{P}(Y~|~W, Z)\]By Decomposition ppty
\[\Rightarrow \mathbb{P}(X, Y~|~Z,W) = \mathbb{P}(X~|~ W,Z)\mathbb{P}(Y~|~W, Z)\] \[\Rightarrow (X\perp Y~|~ W,Z)\]Discussion:
Graph theory point of view:
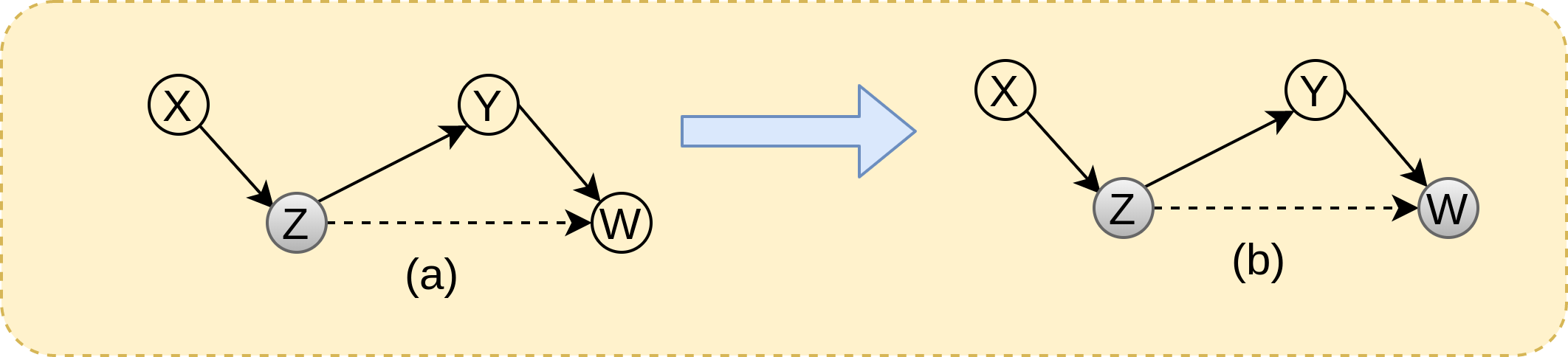
-
condition 1: \((X\perp W, Y~/,Z)\) implies there doesn’t exist any active trail running from X to W and Y in the universe where Z is known (or given)
-
In the below figure, (a) shows the graph incorporating above conditional independency
-
Once if X is independent of Y and W on observing Z, implies X is still independent of Y on observing Z and W
-
This will just add additional conditioning variables which will doesn’t add any additional active trails in the graph
-
The resulting graph is equivalent to that shown in subfigure (b)
Intersection
Given:
\[(X\perp W~|~Z,Y) ~\&~ (X \perp Y~|~Z, W)\] \[(X\cap W\cap Z\cap Y) = \phi\]To show: \((X \perp Y, W ~|~Z)\)
Proof:
Based on the given conditions and disjoint property:
\[\mathbb{P}(X~|~Z,W) = \mathbb{P}(X~|~Y, W, Z) = \mathbb{P}(X~|~Y,Z)\]By Bayes thm:
\[\frac{\mathbb{P}(X,W~|~Z)}{\mathbb{P}(W~|~Z)} = \frac{\mathbb{P}(X,Y~|~Z)}{\mathbb{P}(Y~|~Z)}\]Above Bayes rule holds only if \(\mathbb{P}(Z) > 0\)
Now, by marginalizing above equation over \(W\) we get:
\[\mathbb{P}(X~|~Z)\mathbb{P}(Y~|~Z) = \mathbb{P}(X,Y~|~Z)\] \[\Rightarrow (X\perp Y~|~Z)\]Again by Bayes rule:
\[\mathbb{P}(X,Y,W~|~Z) = \mathbb{P}(X~|~Y,W,Z)\mathbb{P}(Y,W~|~Z)\]Above equation and given conditions we get:
\[\Rightarrow \mathbb{P}(X,Y,W~|~Z) = \mathbb{P}(X~|~Z)\mathbb{P}(Y,W~|~Z)\] \[\Rightarrow (X\perp Y,W ~|~Z)\]Discussion:
Graph theory point of view:
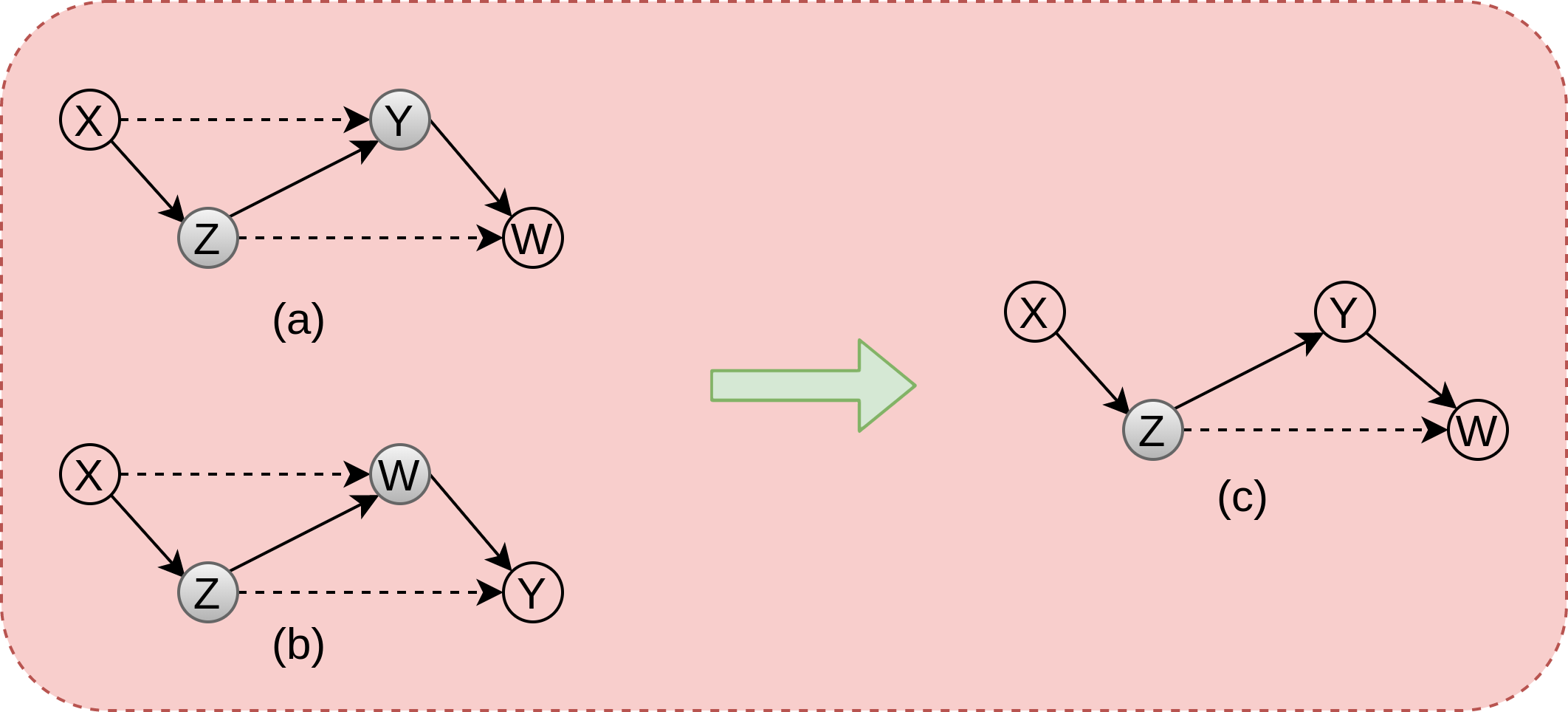
-
condition 1: \((X\perp W~/~Y,Z)\) implies there doesn’t exist any active trail running from X to W in the universe where Z and Y are known (or given)
-
In the below figure, (a) shows the graph incorporating above conditional independency
-
condition 2: \((X\perp Y~/~Z, W)\) implies there doesn’t exist any active trail running from X to Z in the universe where Z and W is known (or given). Subfigure (b) shows the graph incorporating this conditional independence
-
Based on above two conditions as Y and W can be interchanged which means Y and W are disjoint and there can’t exist direct link from Y and W, which results in subfigure (c)
-
In the subfigure (c), there doesn’t exist any active trail from X to Y, W, once Z is known. Which results in CI \((X\perp Y,W~/~Z)\)
Leave a Comment